题目
【2024·嘉峪关市酒钢三中1月联考预测卷:21. (2)】$g\left ( x \right ) = x\ln_{}{\left ( x+1 \right ) } +a\ln_{}{\left ( x+1 \right ) } -x$ ,$g\left ( x \right )$ 在 $\left ( 0,+ \infty \right )$ 单调递增,求 $a$ 的取值范围.
大做法
解析
$g\left ( x \right )$ 作为一个十分复杂的函数,通过直接观察的方式显然不能有所突破,因此,考虑 $g\left ( x \right )$ 的导函数 ${g}’ (x)$ .$g(x)$ 在 $(0,+ \infty)$ 单调递增的等价命题是: ${g}’ (x)$ 在 $(0,+ \infty)$ 上非负.
因此,题目求解的是命题 $p : \forall x\in (0,+\infty)$ ,${g}’ (x) \ge 0$ 为真时,$a$ 的取值范围.
${g}’ (x) = \ln_{}{(x+1)} + \dfrac {a-1}{x+1}$ .
所以命题
$p : \forall x \in (0,+\infty)$ ,${g}’ (x) =\ln_{}{(x+1)} + \dfrac {a-1}{x+1} \ge 0$ .
当前的目标是求得使该命题为真的 $a$ 的取值范围.
${g}’ (x)$ 的性质仍然不是很明显,因此对 ${g}’ (x)$ 求导:
${g}” (x) = \dfrac {1}{x+1} + \dfrac {-(a-1)}{(x+1)^{2}} = \dfrac {x-a+2}{(x+1)^{2}}$ .
${g}” (x)$ 是 ${g}’ (x)$ 的导函数,考察 ${g}” (x)$ 来观察 ${g}’ (x)$ 的性质.
令 ${g}” (x) = 0$ ,得到 $x = a-2$ .即 ${g}’ (x)$ 的驻点是 $a-2$ .这时需要讨论该驻点是否在定义域 $(-1,+\infty)$ 内,先讨论在定义域内的情形,即 $a-2 > -1$ ,$a>1$ .当 $x<a-2$ 时,$x-a+2 < 0$ ,所以 ${g}” (x) < 0$ .当 $x>a-2$ 时,$x-a+2>0$ ,所以 ${g}” (x) > 0$ .所以 ${g}’ (x)$ 在驻点左侧单调递减,在驻点右侧单调递增.
当驻点小于或等于 $-1$ 时,可以说 ${g}’ (x)$ 在定义域内无驻点.此时 $a-2 \le -1$ ,$x-a+2 \ge x+1$ ,$\dfrac {x-a+2}{x+1} \ge 1$ ,所以 ${g}” (x)$ 在定义域内恒大于 $0$ ,${g}’ (x)$ 在定义域内为增函数.
由上总结 ${g}’ (x)$ 的两种单调性:
- 当 $a-2>-1$ 即 $a>1$ 时,${g}’ (x)$ 在 $a-2$ 左侧减,右侧增(图1).
- 当 $a-2 \le -1$ 即 $a \le 1$ 时,${g}’ (x)$ 在定义域上增(图2).
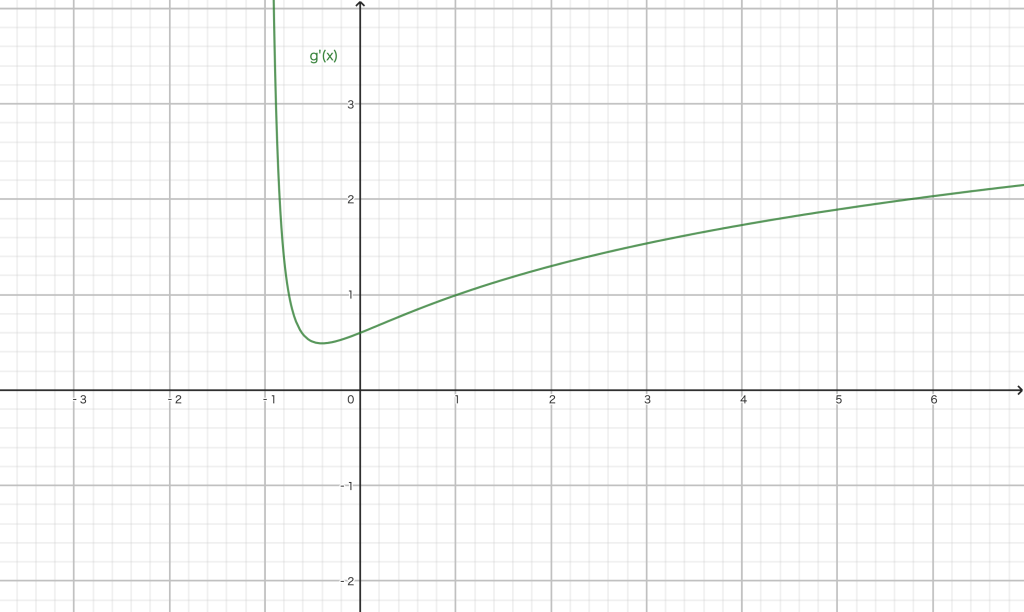
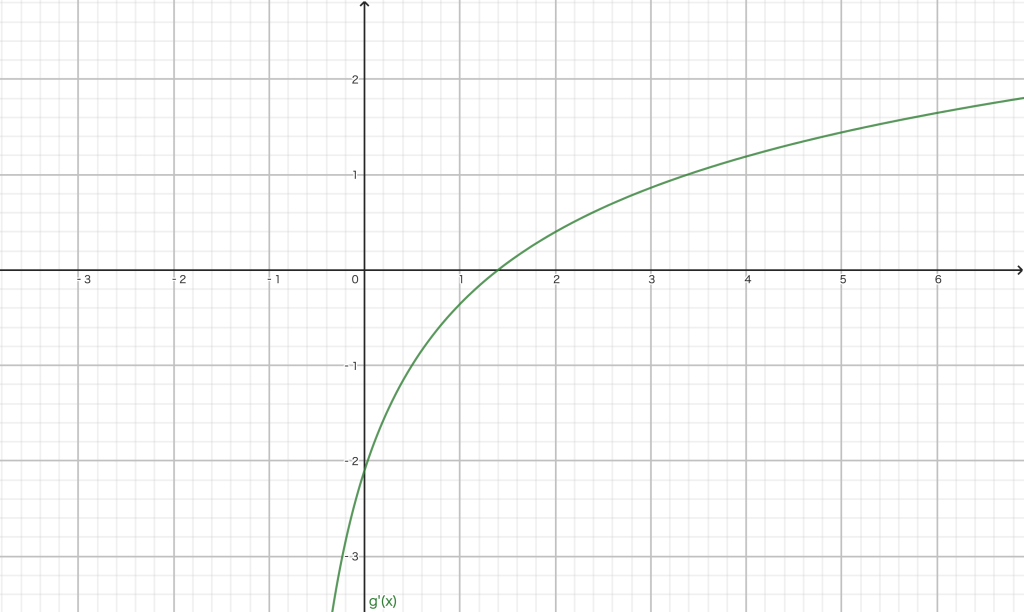
注意到我们要求的是命题 $p : \forall x\in (0,+\infty)$ ,${g}’ (x) \ge 0$ 为真时,$a$ 的取值范围.
显然,对于 $a-2 \le -1$ 即 $a \le 1$ 的情况,由于 ${g}’ (x)$ 在定义域上增,故在 $(0,+\infty)$ 上也增,因此只需使 ${g}’ (0) \ge 0$ ,就可以使命题 $p$ 为真.所以 ${g}’ (0)=a-1 \ge 0$ ,$a \ge 1$ .结合 $a \le 1$ 的前提,得 $a=1$ .
$a-2>-1$ 即 $a>1$ 的情况比较复杂,可以分为两种情况去讨论.第一,当 $-1<a-2 \le 0$ 即 $1<a \le 2$ 时,${g}’ (x)$ 在 $(0,+\infty)$ 上是增的,因此只需 ${g}’ (0) \ge 0$ 即可满足命题 $p$ ,解得 $a \ge 1$ ,结合前提得 $1<a \le 2$ .第二,当 $a-2>0$ 即 $a>2$ 时,${g}’ (x)$ 在 $x=a-2$ 处取得最小值,故只需 ${g}’ (a-2) \ge 0$ 即可满足命题 $p$ ,${g}’ (a-2)=\ln_{}{(a-1)}+\dfrac {a-1}{a-1}=\ln_{}{(a-1)}+1 \ge 0$ ,$\ln_{}{(a-1)} \ge -1$ , $a \ge \dfrac {1}{\mathrm{e}} +1$ ,结合前提得 $a>2$ .
综上,列出满足 $p$ 的三个条件:
- $a=1$ .
- $1<a \le 2$ .
- $a>2$ .
这三个条件涵盖了所以可能的情况,取并集即可.综上,得出结论:
当 $a \ge 1$ 时,$g\left ( x \right )$ 在 $\left ( 0,+ \infty \right )$ 单调递增.
总结
本题研究的是函数的值域问题.由于函数较复杂,需要通过导数来考察函数单调性.过程中需要研究的问题是:函数是不是单调的?在何种情况下是单调的?何种情况下不是?最大值、最小值是多少?在何处取得?等等.虽然使用了二阶导数,但本质上仍然是普通的导数应用问题.必须要关注的是逻辑关系及分类讨论的重要性.
班门弄斧,望不吝批评指教!
小做法
要求的仍然是 $\forall x\in (0,+\infty)$ ,${g}’ (x) \ge 0$ 时 $a$ 的取值范围,即 $\ln_{}{(x+1)}+\dfrac{a-1}{x+1} \ge 0$ 时 $a$ 的取值范围.
对于 $x\in (0,+\infty)$ ,$\ln_{}{(x+1)}$ 是恒正的.$\dfrac{a-1}{x+1}$ 则有两种情况:第一,当 $a-1 <0$ 即 $a<1$ ,$\dfrac{a-1}{x+1}$ 恒为负.第二,当 $a-1 \ge 0$ 即 $a \ge 1$ ,$\dfrac{a-1}{x+1}$ 恒非负.
如图3,对于 $x\in (0,+\infty)$ ,当 $a-1 <0$ 时,其他点暂且勿论,单看 $\lim_{x \to 0^{+}} \ln_{}{(x+1)}+\dfrac{a-1}{x+1} < 0$ ,就知道 $a-1 <0$ 不满足这个命题.而 $a-1 \ge 0$ 显然是满足的,因为两正数相加结果一定为正数.故只需使 $a-1 \ge 0$ 即可使命题为真.
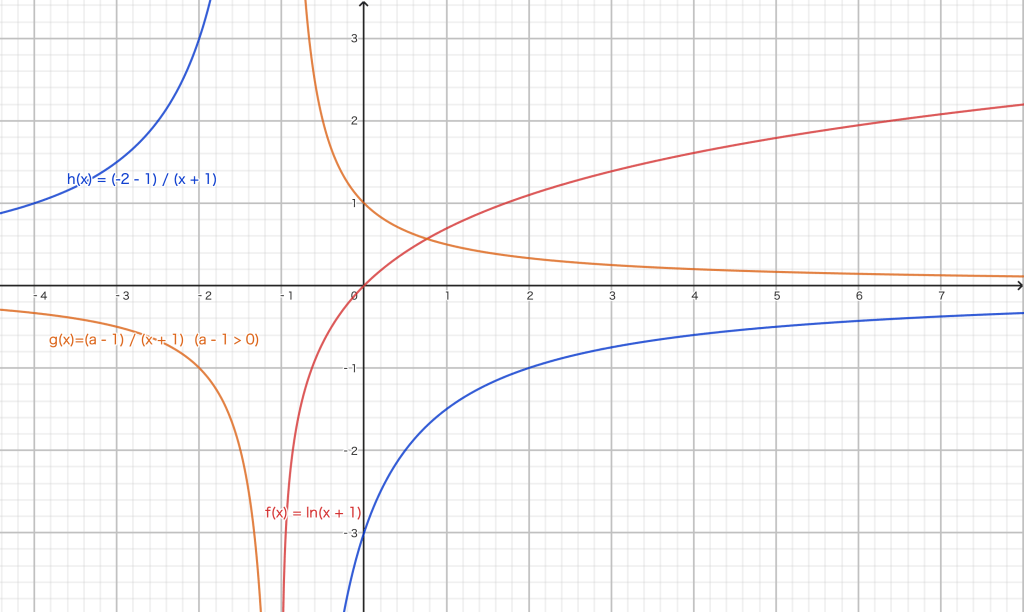
该做法相当巧妙简洁,在考场上能够节省大量时间,是绝大多数学生采用的做法.
题不要多做,要做精、做透,研究得清清楚楚。
——@nanmu